
Goal: Move the center of mass in a stack of wood to a given coordinate.
How can I be as true to the concept of relocation of mass a possible?
How can I convey the process visually in the final product?
In other words, how can I complete the task with the greatest amount of purity? Maybe I can do this through controling my process: limit distractions (such as beautification), distill to clarify, make each move delibrately and consciously, work transparently.

Method of Calculation (aka Design):
There are two different types of panels, each panel becomes two parts through the introduction of a cut line.
One pannel must maintain the complete perimeter of the origional mass. The second pannel must maintain a minimum of half the peremeter. (These restrictions are necessicary for visual continuity between the origional and product.) 1"x1"x0.5" volumes of the panels will be distributed on either side of the cut line to alter the center of masses of each part. The averages of the center of masses of each part must equal the approximate given coordinate within reasonable measure.
There are two different types of panels, each panel becomes two parts through the introduction of a cut line.
One pannel must maintain the complete perimeter of the origional mass. The second pannel must maintain a minimum of half the peremeter. (These restrictions are necessicary for visual continuity between the origional and product.) 1"x1"x0.5" volumes of the panels will be distributed on either side of the cut line to alter the center of masses of each part. The averages of the center of masses of each part must equal the approximate given coordinate within reasonable measure.
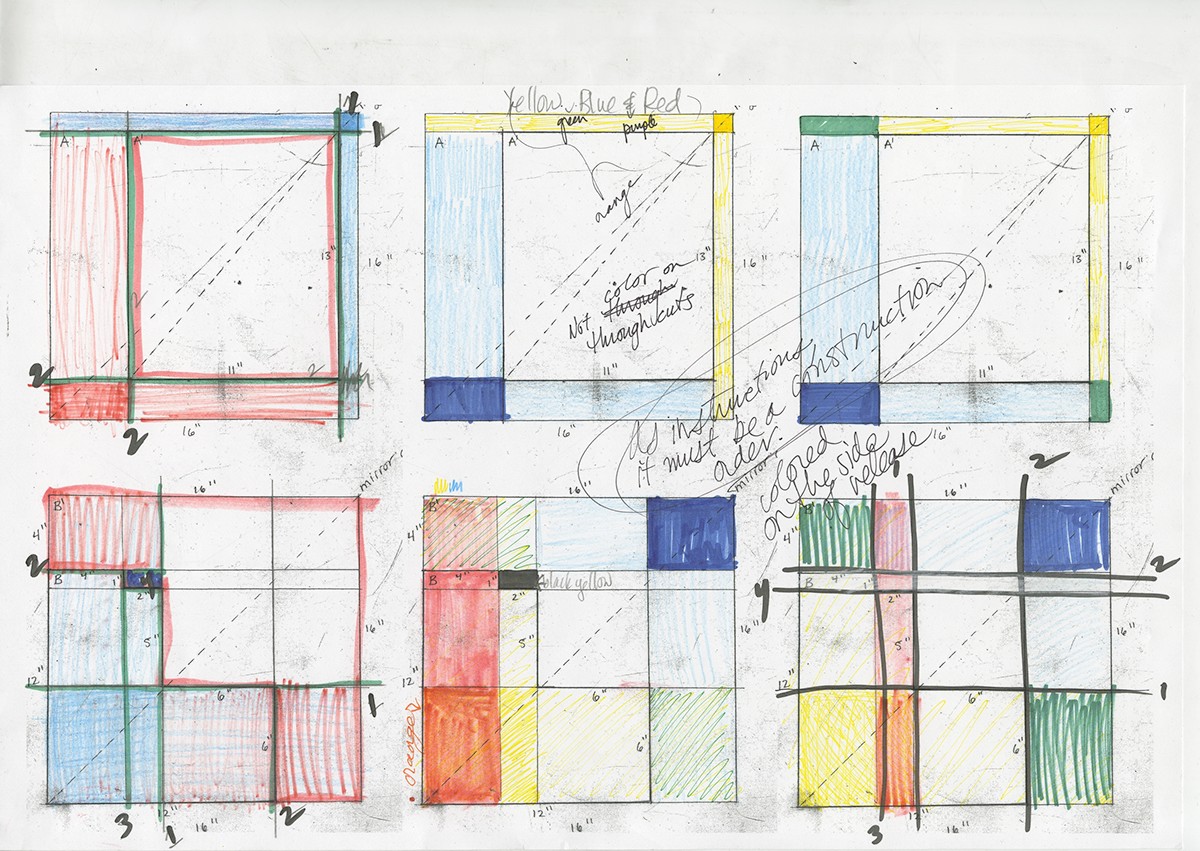
Conveying the Process Visually in the Product:
How can I keep the concept's clarity and transparency in representation? I can control the look more than the materials. Modernist architects have the same delema, so they hide the construction with with walls and call what is left visuble pure. How can I incorperate the construction into the understanding of the concept as much as possible?
My solution to this challange was to build with a minimum of passes through the table saw. I optimized the order of the cuts to minimize the amount of loose pieces. Once the two parts from each panel were free of each other and individually assembled, I created a color geneology to illistrate the the optimization and mathmatical process of for moving the mass. Below is the sketch recording the evolutioin of color:


How does my product fail to be pure?
>The math involved many itterations of trial and error to achieve an accurate balance of mass. A geometeric proof that gave a single solution would have been more successful. I should have included rules of process beyond the basic scientific method to stream line it.
>The ordering of the stacks was not established by calculation and it had to be determined through a visual value system. (The rotation and transformation of the pannels was determined through calculation.)
How does my product succeed in being pure?
>Derived from a series of rules.
>Limitation of visual decisions influencing the product.
>Highly curated thought process and awareness of results of each move.
